Table of Contents
What is the quadratic formula?
Equation for the quadratic formula?
How to identify quadratic equations?
Common mistakes when solve quadratic equations
Example of using the quadratic formula
Quadratic formula applies in real life
Pros and cons of three methods to solve quadratic formula
A self-test: do you know which graphs are quadratic functions?
The quadratic formula is used to solve quadratic equations of the standard form, ax2 + bx + c = 0 where a, b and c are constant values with the unknown x.
The quadratic formula just like trinomial factoring and completing the square is used to determine the roots of a function. Recall, the roots are the points where the function touches the x-axis where the corresponding y value is equal to zero. Hence, for the quadratic formula to work, it is important that the function is set to zero.
For example: Given the quadratic equation:
ax2 + bx = - c.
First, set the equation equal to zero by bringing the c to the left side.
Equation for the quadratic formula
The quadratic formula is as follows:
where a is the coeffcient of the x2 b is the coeffcient of the x and c is the number without any variable beside it.
How to identify quadratic formula?
- 1. The prerequisite to become a quadratic equation is the equation must include “=” sign.
- 2. Since this is a quadratic equation, we have to make sure ax^2 is not equal to 0 that means a cannot be 0.
- 3. b can be any numbers. It is fine that b equals to 0.
- 4. the quadratic equation is not required to have constant numbers.
Checklist:
1. Does the component x^2 appear somewhere in the equation?
2. Does the equation have any other components except x^2? If there are only X term and constant numbers, then the equation is good to solve, but if the equation has other terms, such as x^3, that means the equation doesn’t meet the quadratic formula requirements.
Examples:
1. Is x^2+5=5x a quadratic equation?
Yes! X^2 appears in the equation. The equation has constant number, x term, and no other components. Checklist is done!
2. Is x^3+3x^2+4=0 a quadratic equation?
! x^2 shows up in the equation but the equation also has x^3 which shouldn’t be a part of quadratic formula. This equation doesn’t meet rule 2.
Common mistakes when solve quadratic functions
Here is an example:
X^2-8x-4=0
X(x-8)=4
X=4 or x=12
This is wrong!
The step of moving 4 to the right is useless. When we solve quadratic equations, we prefer to move all terms to the left and keep the right side of the equation equal to 0. For the second step, we assumed that x and x-8 are equal to 4, but this is wrong. We use the above steps to solve quadratic equations only when the constant number is equal to 0. If the quadratic formula is x^2-8x=0, then we can abstract x to the front. The equation will be x(x-8)=0. The answers will be x1=0 or x2=8.
Here are two ways to solve the above question.
1. 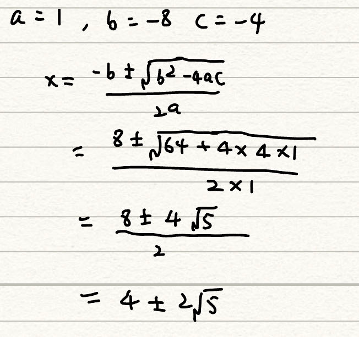
2. 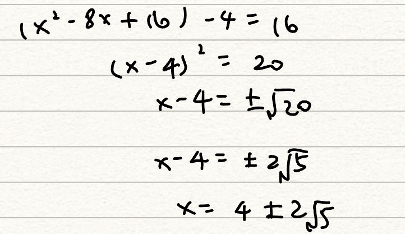
Quadratic formula applies into real life:
Quadratic formula is very useful and can be widely applied to different subjects, such as commerce, engineering, science, etc. They are helpful in forecasting the moving objects’ trajectories, business profits, and the efficiency of transforming inputs into outputs.
Here is an application example:
A shot-put throw’s distance can be predicted using the equation y=-0.5x^2+x+4, where x measures distance while y measures height. What was the distance for the throw?
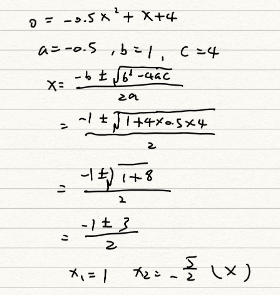
Explanation:
We set y=0 first because the ball will hit the ground. That’s the point where y is equal to 0. We distinguish a, b, and c, respectively, and substitute them in the quadratic formula. As a result, we got two answers, 1 and -2.5. Since we know the distance can’t be negative, so 1 is the only answer to this question.
Pros and cons of three methods to solve quadratic formula
1. Factoring: factoring aims to divide a quadratic formula into two linear equations, such as (hx+t)(qx+r)=0, while h,t,q, and r are constant numbers. The advantage of using this method is that factoring is fast and convenient if answers are integers, but on the other hand, not all quadratic formula can be factored, so you might not be able to get answers by only using factoring.
2. Completing the square: This method requires multiple steps. The main idea is to convert the original quadratic formula into the form of (x+a)^2=b, where a and b are constant numbers. You have to calculate the number and add/subtract it to make the equation become the desired form. The disadvantage of this method is that the calculation is complicated, and easy to get wrong numbers, but it can help you have a better understanding of quadratic formula.
3. Quadratic formula: this method is commonly used because it is easy to apply, and it always works. However, it can’t help you know deeper about quadratic formula. There is no deep insight into solving quadratic functions by using formulas.
A self-test: do you know which graphs are quadratic?
This video will make you walk through different forms of quadratic formula that we will encounter in the real life
A brief introduction to help you have a better understanding of quadratic formula through graphs.
Example of using the quadratic formula
1. Determining two roots using the quadratic formula
Note the quadratic formula has the symbol ±. This means there are two possible values of x hence it is possible to have two roots of a quadratic function.
Example: Solve using the quadratic formula
5x2 + 6x + 1 = 0
Here: a = 5 b = 6 c = 1
Hence, the two roots of the quadratic function are x = 
2. Setting the equation to zero to use the quadratic formula
Example: Solve using the quadratic formula
x2 = 3x – 1
recall: to use the quadratic formula the quadratic equation must equal to zero.
Hence, we can move the 3x and -1 to the left side of the equal sign.
x2 – 3x + 1 = 0
Notice, there is no number in front of x2 so the coefficient must be 1. Also, we include the sign in front as part of the coefficient.
The b must be – 3 (not just 3).
a = 1 b = -3 c = 1
plugging the values into the quadratic formula:
The two roots of the quadratic function are: 
3. Turning the equation to standard form to use the quadratic formula
Example: f(x) = -2(x+6)2 + 4
The quadratic equation of the vertex form must be expanded first into standard form.
Finding the greatest common factor (GCF) results in smaller values for a, b and c hence.
a = 1 b = 12 c = 34
Therefore, the roots of the function: 
4. The quadratic function may have only one root
Example: Solve using the quadratic formula
2x2 + 4x + 4 = 0
In this scenario, the value under the square root is zero hence adding or subtracting the value makes no difierence. There is one root of the function 2x2 + 4x + 4 = 0 at x = -1.
5. The quadratic function may have zero root
Example: y = 3x2 + 4x + 2
a = 3 b = 4 c = 2
Since a square root of a negative number is undefined and does not result in a real number. Hence, in this case we are adding and subtracting a number that does not exist with the – 4. Therefore, the function has no real roots.
Take home points for using the quadratic formula
1. Make sure the given function is a quadratic equation Ex. Given y = x + 1. We cannot solve for x using the quadratic formula since it is a linear function
2. The function must be of the form: ax2 + bx + c = 0
3. Set the equation equal to zero before inputting values for a, b and c
4. Factor the “a” if possible, to work with smaller numbers
FAQ on quadratic formula
a) A standard form of quadratic formula can be y=ax2+bx+c, where a≠0
b) A vertex form of quadratic formula can be y=a(x-c)2+k, where a≠0 and (c,k) will be the vertex of functions.
c) A factor form of quadratic formula can be y=a(x1-e)(x2-d), where a≠0. x1 and x2 will be solutions of equations when y=0.
French mathematician François Viète invented the symbolism in late 1500s, while René Descartes published the book La Géométrie in 1637. It contains the quadratic formula that is still being used today.
Basically, parabola tells us that a curved line faces upwards or downwards. Based on that, we are able to know the vertex is at the highest position or the lowest position of a curve.
Yes, rainbow is a parabola. The rainbow is curved because it is reflected of the sun through raindrops.
It depends on the sign of the leading coefficient, which is a in the quadratic formula. If a is positive, then it means the parabola opens up and the vertex is the lowest point of the curve. Otherwise, vice versa.
Arched bridges, a smile, shape of bananas…….
at your neighbourhood
*Note that Queen Elizabeth Academy offers in class learning at our Mississauga location, at Unit 5, 1020 Johnson’s Lane. The rest of the locations we offer credits online via Zoom (TM) with live teaching.





































